limites de funciones trigonométricas
Qué es un límite? Son los valores que toma una función dentro de un intervalo que se van aproximando a un punto fijo c. Se dice que el límite de la función f (x) es L cuando x tiende a c y se escribe:
Teorema: Si c es un número real en el dominio de la función trigonométrica indicada, se cumplen los siguientes límites de funciones trigonométricas:
Cuando calculamos límites de funciones trigonométricas es necesario recordar las siguientes identidades básicas:
- Sen 2 x + Cos 2 x = 1
- Tan x = Sen x/Cos x
- Cot x = 1/tan x = Cos x/Sen x
- Sec x = 1/Cos x
- Csc x = 1/Sen x
- Sen (α + β) = Sen α Cos β + Cos α Sen β
- Sen (α – β) = Sen α Cos β – Cos α Sen β
- Tan (α + β) = (Tan α + Tan β)/ 1 – Tan α Tan β
- Tan (α – β) = (Tan α – Tan β)/ 1 + Tan α Tan β
- Sen 2α = 2 Sen α Cos α
- Cos 2α = Cos 2 α – Sen 2 α = 2Cos 2 α – 1 = 1 – Sen 2 α
- Tan 2α = 2 Tan α / 1 – Tan 2 α
Veamos ahora dos límites que podemos llamar especiales y que sonde gran utilidad al evaluar límites de funciones trigonométricas:
- Límite especial 1
Si medimos el ángulo θ en radianes y sabiendo que nuestro denominador no puede ser cero, realizamos una tabla de valores con valores próximos a cero:
-0.4
|
-0.3
|
-0.2
|
-0.1
|
-0.01
|
0
|
.01
|
0.1
|
0.2
|
0.2
|
0.4
|
0.973
|
0.985
|
0.993
|
0.998
|
0.999
|
f (x)
|
0.999
|
0.998
|
0.993
|
0.985
|
0.973
|
Podemos deducir entonces que:
2. Segundo límite especial
Recordando que el coseno de cero grados vale 1, obtendríamos una indeterminación 0/0, entonces para eliminar la determinación multiplicamos por su conjugada y aplicamos las identidades:


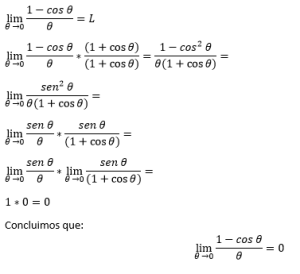

No hay comentarios:
Publicar un comentario